weasel의 우당탕탕 개발기

이전편 : 페이징

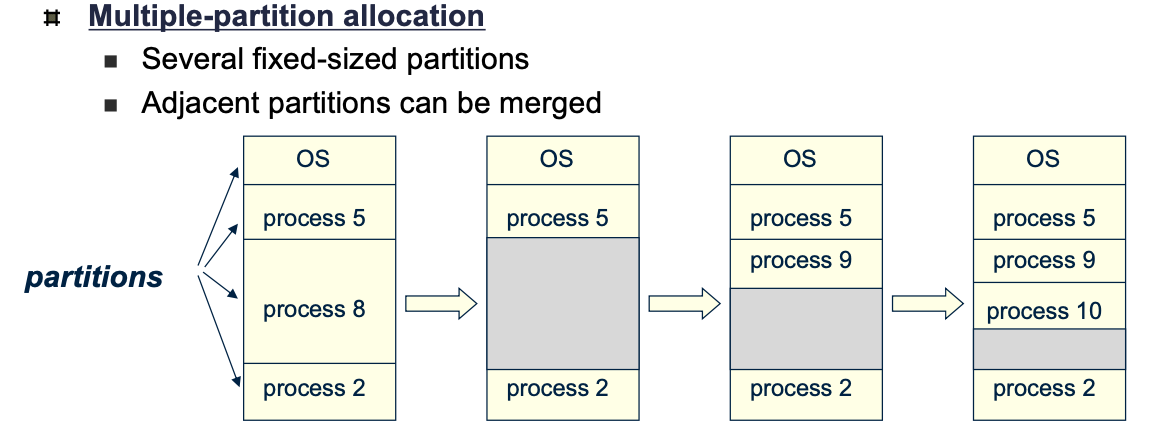
가상 메모리 (Virtual Memory)

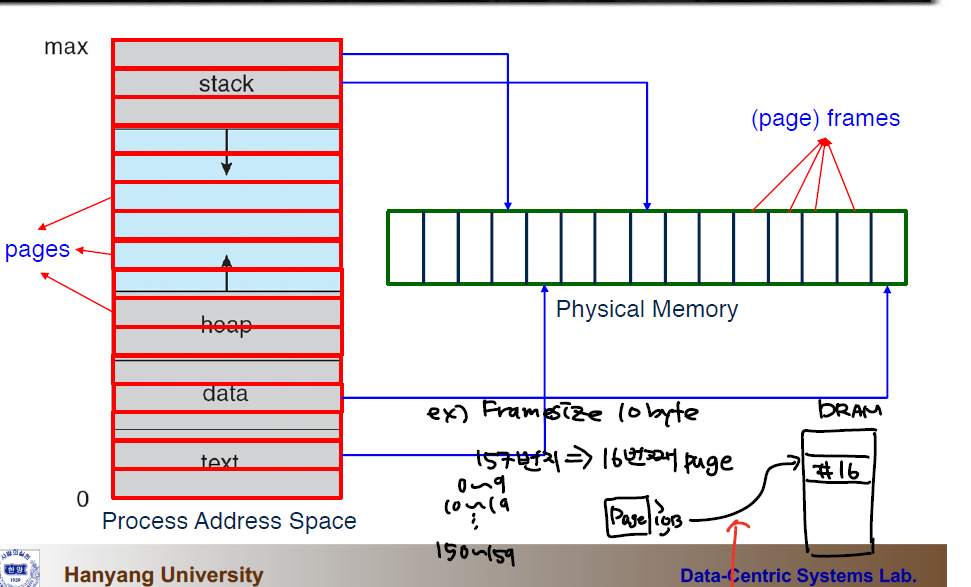
가상 메모리는 논리적 메모리와 물리 메모리를 분리시켜, 프로세스 전체가 메모리내에 올라오지 않아도 실행가능하도록 하는 기법이다.

물론 프로그램이 실행되기 위해서는 메모리에 프로세스가 올라와야 하는것은 맞다. 하지만 특정 부분을 실행할때는 그 부분만 메모리 위에 올라와있어도 구동이 된다.

그렇기 때문에 논리적 주소공간은 실제 물리적 주소공간보다 훨씬 커도 된다. 왜냐면, 어차피 일부만 실행할때 필요하니까..
그럼 가장 핵심적인 기술은 프로세스를 실행할때, 필요한 메모리를 불러오고(swapped in) 필요하지 않은 부분은 내리는(swapped out) 과정이 필요하다.

가상메모리는 요구 페이징(Demand Paging) 이라는 기술로 구현된다.

특정 페이지에 대한 수요가 있을때, 즉 페이지에 대한 참조 요청이 들어왔을때 페이지를 메모리로 불러오는것이다.

다시 말해서 기존의 방법과는 다르게 가상 메모리 방식을 취하면, 시작할때부터 아무 메모리도 올라와있지 않아도 되고 필요할때만 불러오는 방식이다.

프로그램에서 사용되는 일부분만 메모리에 적재하는 가상 메모리를 통해서 아래와 같은것들이 가능하다.

• 시스템 라이브러리가 여러 프로세스 사이에 공유가 가능하다.
  프로세스 입장에서는 자신의 주소공간에 라이브러리가 올라와있다고 생각하지만, 실제로 라이브러리가 들어 있는 물리 메모리는 하나로 모든 프로세스에 공유되는 방식이다.
• 프로세스가 만들어질때 훨씬 더 효율적이다. 왜냐면, 실제로 프로세스를 만들때 필요한 모든 메모리를 할당해주는것이 아니라 필요할때만 주기 때문에 훨씬 가볍고 효율적이다.
  • 예를 들어서 fork 를 해서 프로세스를 생성한다고 해보자.
    이때 메모리를 직접 주는것이 아니라 기존의 메모리를 그대로 사용하게끔만 하고 프로세스는 이것을 독립적인 메모리 공간으로 인식한다.
• 실제 물리 메모리보다 더 큰 메모리를 요구하는 프로세스를 구동시킬 수 있다.
• 더 많은 프로세스가 구동이 가능하다.

요구 페이징 (Demand Paging)

페이지를 메모리에 올릴때 오직 그것이 필요할때만 수행하는것을 요구 페이징이라고 한다.
이것을 Lazy Swapper이라고도 하는것같다.(그 페이지 필요할때까지 절대 페이지를 메모리에 올리지 않는다)

• 적은 I/O : 전체 코드내에서 접근 안되는 주소공간은 가져올 필요가 없으니.
• 적은 메모리 사용량
• 빠른 응답 : 모든 페이지가 올라와있을 필요가 없으니 시작이 빠르다.
• 더 많은 유저 : "논리적 메모리 >> 물리적 메모리 " 이니 더 많은 프로세스를 수용가능하다.

만약에 특정 페이지가 필요하다고 하자. 그럼 그 페이지를 참조해야하는데, 아래와 같은 분기를 가지게 된다.

• 페이지에 대한 잘못된 참조 → 에러
• 메모리에 올라와있지 않음 → 데이터를 메모리에 적재함

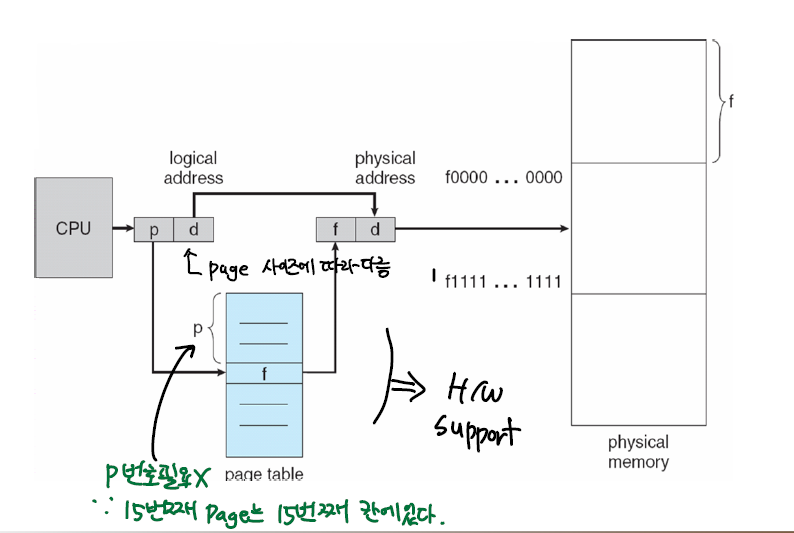
그럼 이 올라와있지 않거나 올라와 있는것을 어떻게 구분할까?

논리주소와 물리주소를 변환할때 쓰였던 페이지 테이블을 이용해 페이지 테이블의 엔트리에 valid-bit를 부착해서 구분한다.

만약 valid-bit가

• True면
  • 현재 그 메모리를 가져온다.
• False면
  • Page Fault 발생
  • Page fault에 대한 처리를 하는데 일반적으로 페이지에 해당하는 프레임을 찾아서 로드시킨다.
    

    

    
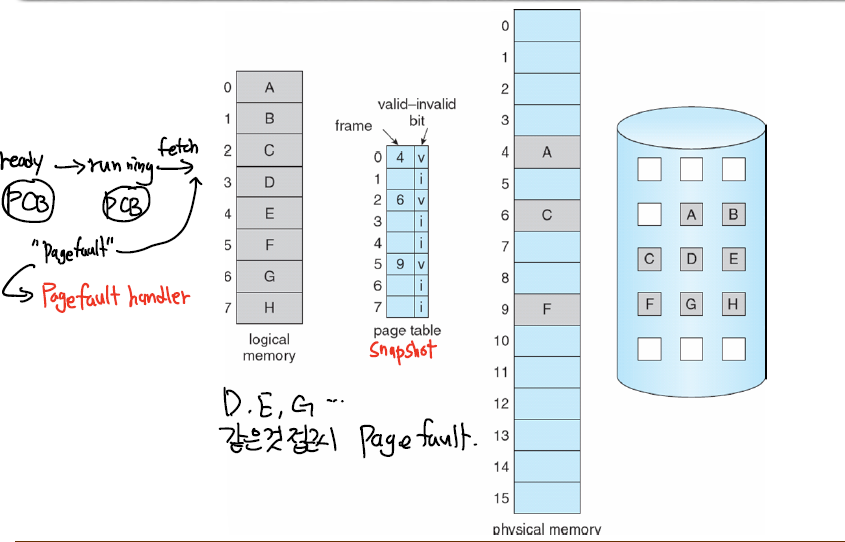
    위 그림을 보면 B,D,E,F,G,H는 valid-bit가 invalid로 되어있다.
    만약 이때 B나 F와 같은 페이지를 참조하려 하면 Page Fault가 일어나는 것이다.

그럼 페이지 폴트 (Page Fault)가 뭘까?

페이지 폴트 (Page Fault)

페이지 폴트는 valid-bit가 invalid 인 곳에 MMU가 접근을 할때 HW trap을 발생시키면서 생긴다.

valid-bit가 invalid 하다는 것은 현재 메모리안에 내가 원하는 페이지가 존재하지 않음을 의미하므로, 원하는 페이지에 해당하는 프레임을 메모리로 가져온 후 프로그램이 계속 동작되게끔 해야한다.

이것을 페이지 폴트 핸들링이라고 한다.

페이지 폴트 핸들링

페이지 폴트는 결국에 인터럽트이기 때문에 ISR을 수행하는 처리과정을 거친다.

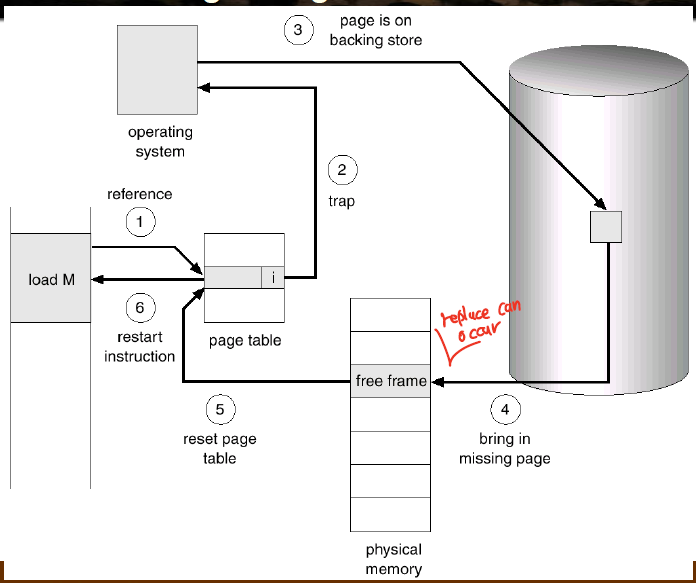
아래는 프로세스가 특정한 페이지를 참조하려고 했을때의 과정에 Page Fault 핸들링하는 과정이 추가된것이다.

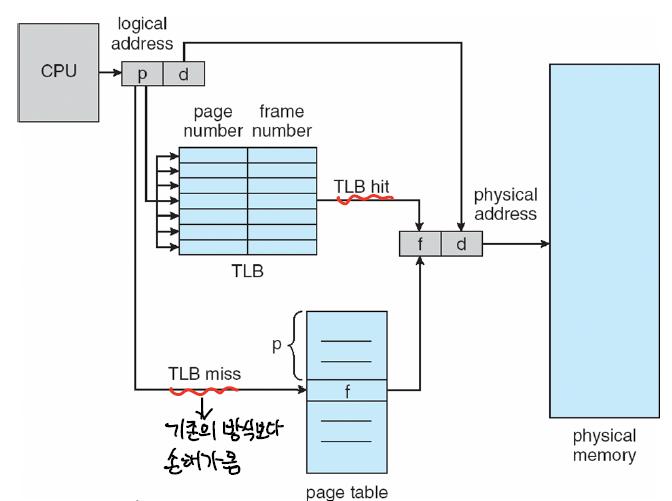
1. 프로세스가 논리주소 (p,d) 를 가지고 메모리에 접근하려고 시도한다.
2. TLB를 먼저 확인해서 p에 해당하는 프레임 번호 f가 있는지 확인한다.
   1. TLB Hit,있다면 바로 메모리로 접근해서 (f,d)를 가져온다.
   2. TLB Miss, 없으니 이제 페이지 테이블을 참조해야 한다.
3. (p,d)를 가지고 페이지 테이블에 접근한다.
   1. 페이지 테이블에 p에 해당하는 f가 valid하면, 메모리에 접근해서 로드한다.
      • 이때 TLB 엔트리도 갱신된다.
   2. 만약 valid하지 않다면 현재 메모리에 올라와있지 않다는 것 → Page Fault
4. 운영체제가 메모리 접근할때의 주소를 확인한다.
   1. 잘못된 접근인가? 그러면 중지시켜야 한다.
   2. 아니라면 진행.
5. 물리 메모리에서 적절히 빈공간을 찾는다.
   1. 만약 이때 없다면, 적절하게 다른 프레임을 교체시켜야 한다. 이 교체의 방식이 매우 중요한데, 잘 골라야 다음에 replace가 일어날 확률을 줄인다.
6. 저장소에서 매치되는 페이지를 프레임에 올린다.
   1. 이때 프로세스는 wait 상태인데, 저장소 접근 자체가 I/O 이기 때문이다. 컨텍스트 스위칭 발생.
   2. I/O가 끝나면, 페이지 테이블 엔트리가 업데이트 되고, valid-bit가 valid로 설정된다. 이때도 컨텍스트 스위칭 발생할것같다.
   3. 프로세스는 레디큐로 옮겨진다. 그리고 일반적으로 스케쥴링되는것처럼 기다려야 한다.
7. CPU를 다시 할당받게 되면 페이지 폴트 트랩 처리가 끝난다.
8. 페이지 폴트를 촉발시켰던 명령어부터 다시 수행한다. (PC를 증가시키지 않기 때문에. 만약 PC 증가시키면 그 명령어는 강제로 건너띄는것이다.)

쓰레싱 (Threshing)

스레싱은 멀티프로그래밍 환경에서 페이지 폴트가 많이 일어나서 시스템이 아무런 작업도 하지 못하고 페이지를 메모리에서 가져오고 빼내는 과정만 반복해 CPU 이용률이 급격하게 떨어지는 현상이다.

더 최악인 점은 CPU 이용률이 떨어지니, 레디큐에 프로세스를 올리는 Long-term scheduler가 판단하기를
”CPU 이용률을 높이기 위해 멀티프로그래밍 정도를 올려야 함"이라고 판단하고 레디큐에 더 많은 프로세스를 올리면서 페이지폴트는 더 늘어간다.

• 여기서 멀티프로그래밍 정도가 느는것과 페이지폴트가 무슨상관일까?
  • 새로운 프로세스가 올라오면, Short-term scheduler가 새로운 프로세스에 CPU를 할당할 것이고, 이때는 initial page fault가 생기기 때문이다.

결국 Swap-in,Swap-out만을 하느라 바쁘고, 프로세스는 Block 되며, CPU는 대부분의 상황에서 IDLE 상태다.

I/O 작업만 하니까..

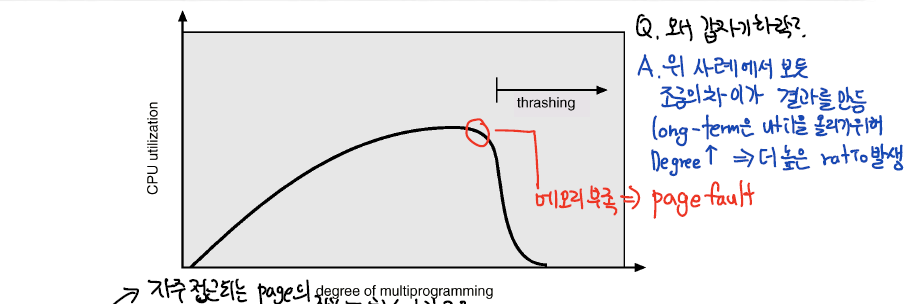
위의 그림처럼 MPD를 계속 올리다보니 스레싱이 발생하고, 그러면 더 MPD를 올리게되고 페이지폴트는 더 자주일어나면서 CPU 이용률은 급감한다.

결국에 자주 접근되는 페이지가 메모리에 올라와있지 않으면 이런 많은 페이지 폴트가 생기는데,
그렇기 때문에 각 프로세스가 필요로 하는 최소 프레임의 개수만큼은 보장을 해주어야 한다.

Array

논리적 저장순서와 물리적 저장순서가 일치한다. 다시 말해서 a[2] 와 다음에 오는 a[3] 는 물리적으로 연결되어 있다.
하지만, 하나의 Array의 크기가 너무 커 하나의 page(혹은 frame) 안에 다 못들어오는 경우에는 virtual adress는 연속적으로 이어져있지만, physical adress에서도 그렇다는 보장은 없다.

💡 하지만 physical adress와 virtual address에 관한 문제는 OS가 처리할 일이고 프로그래머에게 보이지 않는 추상계층이기에 우리가 깊게 생각할 필요는 없다고 생각한다.

또, 한번 사이즈가 정해지면 변할 수 없다. 이를 해결하는 방법이 Dynamic Array다.

• 조회 : 인덱스를 기반으로 한 접근이 가능하다. 인덱스를 알고 있다면 O(1)의 시간 내에 접근이 가능한데 , 이것을 Random Access라고 한다.
• 삽입 : Array의 특정 위치에 삽입을 할때는 원소를 넣고 끝나는 것이 아니라, 기존의 원소들을 shift 해주는 비용이 생기기 때문에 O(n)의 비용이 든다.
• 삭제 : 삽입과 마찬가지로 shift의 비용 때문에 O(n)이 소요된다. 만약 shift를 해주지 않는다면 삭제를 한 곳에 빈 공간이 생기게 될것이고, contiguous한 Array의 특성이 깨진다.

ArrayList

Java 기준으로 primitive만 저장 할 수 있는 Array와는 다르게 Object도 가능하다. ArrayList에 add를 사용하여 primitive한 데이터를 집어넣을때는 Auto-boxing이 사용된다. 또 제네릭이 사용 가능하다.

하지만 가장 큰 차이점은 ArrayList는 Dynamic Array라는 것이다. ArrayList는 내부적으로 Array와 사이즈 정보를 가지고 있다.

Array의 초기 사이즈가 고정되어 있고 늘어나지 않는것에 비해서, ArrayList는 add를 이용해서 원소를 삽입하다가 원소가 가득차게 되면, 내부적인 Array의 크기를 두배 혹은 1.5배 정도로 늘여서 기존의 원소들을 다 옮기게 된다.

이 과정에서의 시간 복잡도를 고민해보면, 기존 원소의 개수가 0개이고 사이즈가 n개라고 해보자.
이때 n번의 add를 할때까지 내부 Array는 가득차지 않고 각각의 삽입연산의 시간복잡도는 O(1)이다.

하지만 한번 더 add를 한다면 내부 Array를 두배로 늘리고 , 기존의 n개의 원소들을 모두 옮겨야 하니 O(n)의 시간이 소요된다.
n+1번의 add에 걸리는 시간복잡도가 O(1)*n+O(n)이니, 평균적인 시간 복잡도는 (O(1)*n+O(n))/(n+1)=O(1)이 되는 것이다.

이것을 분할 상환(Amortized Analysis)라고 한다.

LinkedList

LinkedList는 불연속적인 데이터들의 집합이다. LinkedList는 Node라고 불리는 내부구조들의 chain으로 구성되어 있는데 구조는 아래와 같다.

struct Node {
    Node* next;
    int val;
}

이처럼 Node는 원소와 그 다음 Node를 가리키는 포인터로 구성된다. 각각의 원소들은 오직 자기 다음에 오는 Node의 정보만을 가리키고 있는 것이다.(Singly Linked List 기준). 물론 next 라는 포인터를 하나 더 유지하는 메모리 사용량도 무시할 순 없다.

이것을 이용하여 삽입과 삭제를 O(1)만에 할 수 있다. 삽입을 할때는 단순히 next 만 교체하면 되고, 삭제 역시 마찬가지다.

• 조회 : k번째 원소를 찾기 위해서는 O(k)만큼의 시간이 소요된다.
• 삽입 : 동작 자체만으로는 O(1)이 걸리지만, 원하는 위치를 찾기 위해 LinkedList를 순회해야 하기 때문에 평균적으로 O(n)이 소요된다. 단, 맨 앞에 삽입하는 경우는 O(1)이 소요된다.
• 삭제 : 삽입과 동일. 맨 앞 삭제는 O(1), 맨 뒤 삭제는 tail 에 대한 정보가 있어도 O(n)이 걸리는데 그 이유는 마지막 원소를 가리키는 직전 원소를 찾기 위해 O(n)의 시간이 걸리기 때문이다.

그럼에도 LinkedList가 중요한 이유는 Tree 구조를 이해할때 필수적이기 때문이다.

Doubly Linked List

앞서 살펴본 Linked List는 일반적으로 Singly Linked List를 지칭하는 말이다. Singly Linked List는 아래처럼 다음 원소를 가리키는 next 포인터 하나만을 가지고 있다.

struct Node {
    Node* next;
    int val;
}

이에 반해서 Doubly Linked List는 next 포인터와 그 직전 원소를 가리키는 prev 포인터 역시 가지고 있는 아래와 같은 구조를 띈다.

struct Node {
    Node* next;
    Node* prev;
    int val;
}

또 일반 Singly Linked List와는 다르게 헤드 역시 Node로 이루어져 있다.

• 삽입 : new_node를 삽입하는 과정인데 살펴볼 필요가 있다.

  

  1. new_node의 prev가 before을 가리키게 한다.

  2. new_node의 next가 before의 next를 가리키게 한다.

  3. before의 next의 prev가 new_node를 가리키게 한다.

  4. before의 next가 new_node를 가리키게 한다.

     이 과정에서 순서에 유의해야 하는데, 1번은 언제 일어나도 상관이 없다.
     하지만 2번,3번의 경우 4번보다 먼저 일어나야 하는데, 그렇지 않으면 before의 next가 가리키는 node를 접근 할 방법이 없어지기 때문이다. 또 당연히 첫 순서로 실행되어서는 안된다.

• 삭제 : removed node를 삭제하려는 과정이다. removed의 이중 연결을 해제해주고, removed의 next와 prev를 서로 연결시켜준다.

  

  1. removed의 prev가 removed의 next를 가리키게 한다.

  2. removed의 next가 removed의 prev를 가리키게 한다.

     두 연산은 순서를 바꿔도 상관이 없다.

• 조회 : Doubly Linked List에는 prev 포인터가 있기 때문에, 최악의 경우 O(n)이 소모되었던 Singly Linked List와는 다르게 O(n/2)의 시간 안에 찾을 수 있다. 찾으려는 원소의 인덱스의 범위에 따라 end에서 prev 포인터를 이용해서 돌아가거나, head에서 next 포인터를 이용해 찾는 방법이다. 또, 직전 원소를 찾는 before도 쉽게 구현 할 수 있다.

이런 장점을 이용해서 연속적인 탐색과 접근에 유리하지만 , 구현이 상대적으로 복잡하고 prev 포인터를 유지해야 하기 때문에 메모리 사용량이 2배 정도 증가한다.

하지만 사용성때문에 플레이리스트, 되돌리기와 같은 기능에 사용되는 자료구조다.

Array vs LinkedList

일반론적인 얘기에서 조회는 Random Access를 지원하는 Array가 O(1)의 시간복잡도를 가지고 있어서 LinkedList보다는 빠르다.

삽입과 삭제는 모두 LinkedList가 빠르다고 하지만 이유에 대해서 조금 더 면밀하게 살펴볼 필요가 있다.

빠르다 라고 하는 것은 삽입과 삭제 그 자체에 주목하는 부분이다.
만약 바꿔야 할(삽입 혹은 삭제) 위치를 정확히 아는 상태에서는 Array보다 LinkedList가 항상 빠르다. 단순히 next 포인터만 변경해주면 되기 때문이다.

평균적인 경우에서는 Linkedlist는 O(n/2)개의 원소들을 살펴보아야 하고, Array도 동일한 원소의 개수들을 shift 해줘야하니 비슷하다.

그렇기 때문에 Usage에 따라 두 자료구조를 적절히 아래와 같이 선택해야 한다.

• 삽입과 삭제가 빈번하게 일어나는 경우 → LinkedList
• 데이터에 대한 접근(Access)가 빈번하게 일어나는 경우 → Array

Cache

또 한가지 더 깊게 생각해보자면, 캐싱과 연관이 있다. 정확히 말하면 Spatial Locality.

CPU가 일을 처리할때는 메모리에서 필요한 데이터를 로드하고, 일부를 캐싱한다. 그 캐시 안에 들어있는 요소들을 레지스터로 가져와서 일을 처리하는데, 이 과정에서 차이가 발생한다.

LinkedList는 데이터들의 주솟값들이 서로 연속적이지 않기 때문에, loop를 돌때 (Iterator든 뭐든) 매번 다음 메모리 주소를 찾아야 하고 , CPU가 메모리에 계속적으로 접근해서 로드하는 과정이 생길 수 있다.

불필요한 오버헤드가 생기는 것이다.

반대로 배열은 연결된 데이터 구조를 가지기 때문에, 특정 영역에 존재하는 데이터들을 한번에 로드해와서 bulk들을 캐싱한다.
그렇기에 loop를 돌때도 Array가 매우 크지 않으면 이미 캐시되어 있는 리소스들을 사용할 수 있게 되고 LinkedList와 비교했을 때 상대적으로 적은 메모리 접근이 일어나니 더 빠르다.

운영체제의 핵심 부분인 하나인 메모리 관리에 대해서 적겠다.

대략 3편으로 구성되며 페이징,가상메모리,페이지 교체 알고리즘 순이다.

MMU

CPU는 프로세스를 구동할 때 PC를 참조해서 다음 명령어를 메모리에서 가져온다. 명령어를 참고해 필요한 데이터가 있으면 메모리에서 가져오는데 이때 주소체계가 서로 다르다.

아래의 그림처럼 base와 limit 레지스터 안에 있는 값들을 조합해서 CPU가 사용하는 주소(논리 주소)와 실제 메모리 주소(물리 주소)를 구할 수 있다.

그러면 왜 두 주소를 구분하였을까?

가장 큰 이유는 보안이다. Limit 레지스터를 둠으로써, P1이 P2의 메모리 영역을 참조하는 Memory Illegal Access를 방지하는 Protection의 기능을 수행한다.

MMU는 Memory-Management Unit의 약자로 위에서 말한 논리주소를 물리주소로 대응시켜주는 HW 장치이다.

MMU 방식에서는 relocation 레지스터가 존재하는데, 프로세스가 메모리 주소를 만들때마다 relocation 레지스터 안의 값이 더해지고 이를 통해서 메모리에 접근할 수 있게 된다.

base 레지스터와 역할이 동일하다고 생각하면 된다.

연속적인 할당(Contiguous Allocation)

메모리에 프로그램을 연속적으로 할당하는 방법이다. 간단하게 말해서 아래에서부터 차례차례 채워가는 방식. 메모리를 연속적으로 사용하기 때문에 간단한 MMU만으로 구현할 수 있다.

일반적으로 커널은 낮은 메모리주소에 배치되고, 유저 프로세스는 높아지는 메모리 주소를 가진다.

또 커널을 제외한 메모리 영역을 하나로 보는 방식과 여러개의 파티션으로 보는 방식이 있다.

여러개의 파티션으로 할당하는 방법에서는 다수의 고정된 크기의 파티션으로 나누어져 있고, 2개 이상의 파티션에 할당할때는 합병(merge)해서 할당한다.

그런데 그림에서 마지막 단계를 잘보면 P10과 P2 사이의 빈 공간이 보인다.
이것을 Hole이라고 하는데, 단순히 말해서 할당가능한 메모리의 영역이다.

이 Hole은 크기가 커서 프로세스를 할당받을 정도가 되면 문제가 되지 않지만, 그 크기가 작을때는 파편화 문제가 생길 수 있다.

파편화 (Fragmentation)

파편화 혹은 단편화는 메모리 내에서 할당가능한 영역이 존재하지만, 할당이 불가능한 상태를 의미한다. 두가지 종류가 있다.

• 내부 파편화

  • 할당을 하는 단위가 존재할때 생긴다.

  • 프로그램이 필요한 사이즈보다 더 큰 메모리가 할당되면서 파티션 내부적으로 메모리 공간이 낭비되는 상황

    

• 외부 파편화

  • 남아있는 메모리가 흩어져 있어서 총 메모리 양은 할당할 수 있을 정도인데 실제론 할당할 수 없을때

    

  • 내부 파편화와는 다르게 할당을 하는 단위가 존재해도 생기고, 존재하지 않아도 생길 수 있다.

    • 존재할때는 왜 생길까?
      • B프로세스의 다음 메모리 공간을 보자.
        원래는 프로세스가 들어갈 자리인데도 그 프로세스가 끝나고 D가 끝나지 않았다면 C는 들어가지 못한다.

  • 즉, 사용가능한 메모리 영역은 있는데, 연속적이지 않은것이다.

  • 압축(compaction) 기법을 통해서 해결 할 수 있는데, 오버헤드가 크다. (JVM GC의 mark-and-compaction 생각해보자.)

세그멘테이션 (Segmentation)

페이징 방법에서는 가상 메모리를 서로 같은 크기로 분할했지만, 세그먼테이션 방법에서는 서로 크기가 다른 논리적 단위인 세그먼트로 분할한다.

세그먼트들의 크기가 각각 다르기 때문에(code를 위한것,데이터를 위한것...) 필요할때마다 빈 공간을 찾아서 해결한다.

프로세스가 딱 필요한 만큼만 메모리를 배정해주기 때문에 내부파편화 문제는 없지만, 외부 파편화 문제는 존재한다.

• 아래 그림을 보자. (a)번 상황에서 Segement 1이 빠지고 S7이 들어오면, S7이 더 작기 때문에 공간에는 맞지만 S2와 S7 사이에 빈공간이 생긴다.!
  

  

• 비슷한 상황이 S4가 나가고 S5가 들어오는 상황에서도 생기고 3과 6의 상황에서도 생긴다.
  이런 빈 공간이 생기기 때문에 세그멘테이션은 외부파편화 문제가 여전히 존재한다.

페이징 (Paging)

논리적 메모리 주소 공간이 물리적인 메모리 공간에서 비연속적으로 배치하게끔 허용하는 기법을 의미한다.

물리메모리를 고정된 사이즈의 프레임(Frame) 이라는 크기로 나누고, 동일한 사이즈로 논리메모리를 페이지(Page) 로 나눈다.

즉 , 프로세스가 일정량의 페이지를 요구하면, 같은 양의 충분한 프레임을 찾아서 매치시켜준다. 그렇기 때문에 허용가능한 프레임을 추적해야한다.

또 페이지와 매치되는 프레임을 찾기 위해 페이지 테이블을 관리해야 한다.

하지만 외부 파편화 문제는 해결할 수 있지만(비연속적으로 배치하니) 내부 파편화 문제는 여전히 존재한다.

위의 그림처럼 프로세스의 메모리주소를 같은 크기의 페이지로 나누고 물리 메모리의 프레임과 대응시킨다.

이 대응이라는 것은 논리주소를 단순히 구성할 순 없고, 일반적으로 2^m바이트의 논리 메모리 사이즈와 페이지 사이즈가 2^n바이트일때, 아래와 같이 m 비트를 (m-n)비트,n비트로 구성한다.

페이지 오프셋은 2^n바이트의 페이지 중에서 현재 몇번째 바이트를 지시하는지 알려주고, m-n비트의 페이지 넘버는 페이지 테이블 내에서 몇번째 프레임을 가리키는데 사용된다.

이러한 페이징 방식에서 논리주소 변환은 위의 구조를 가진다.
잘보면 offset인 d는 주소 변환에는 안쓰이고 바로 물리주소에 대응시켜버린다.
반대로 p인 페이지 넘버는 page table내부에서 frame number와 매치시키기 위해서 사용되는데 p→f 의 역할을 하드웨어의 지원을 받아서 수행된다.

페이지 테이블

페이지 번호와 프레임 넘버를 매치시켜주는 구조를 페이지 테이블(Page Table)이라고 하는데 , 메모리 안에 저장된다.

그렇기때문에 실제로 어떠한 메모리에 접근할때는 두 번의 메모리 접근이 필요하다.

1. 메모리에 있는 페이지 테이블 접근
2. 변환된 물리적 주소에 가서 메모리 접근

이 메모리 접근은 꽤 비용이 큰 작업이기 때문에 TLB라는 새로운 하드웨어 캐시가 쓰인다.

TLB

TLB는 Associative Memory라고도 불리는 하드웨어 캐시인데, 논리주소를 물리주소로 변환할때 메모리접근을 줄이기 위해서 사용된다.

페이지테이블과 유사하게 페이지 번호와 프레임 번호가 대응되게 기록되어 있다.
다만, 모든 페이지 번호가 TLB 안에 있는 것은 아니다.

물론 이 레코드들을 다 순차적으로 읽는것은 아니고, 하드웨어의 지원을 받아 병렬적으로 읽기 때문에 매우 빠르다.

이에 관해서 좋은 답변이 있어서 공유한다. How does a TLB lookup compare all keys simultaneously?

요악하자면 단일 CPU 안에서라도 파이프라이닝 기법을 이용해서 병렬적으로 읽는다는 것. (컴퓨터구조 수업을 참고하자.)

TLB가 도입되면서 (p,d)의 논리주소를 물리적 주소로 변환하는 방법이 변했다.

1. TLB를 먼저 확인해서 p에 해당하는 프레임 번호가 있는지 찾는다.
   1. 있다면, 프레임 넘버 f와 오프셋 d를 가지고 바로 메모리에 접근한다.
   2. 없다면 2번으로 간다.
2. 메모리에 있는 페이지 테이블을 확인한다.
3. 페이지 테이블에 적힌 프레임 넘버 f와 오프셋 d를 가지고 메모리에 접근한다.
4. 가장 최근에 사용된 (p,d)→(f,d) 를 TLB에 저장한다.

1,4번 때문에 TLB는 논리적→물리적 주소 변환에서 캐시 역할을 수행한다고 볼 수 있다.

💡 다만 일반적인 CPU 캐시(L1,L2...)와는 목적 자체가 다르다. TLB는 주소 변환 속도 향상을 위한것이어서 MMU에 의한 주소변환시에 생기고 , CPU 캐시는 데이터를 가져올때 메인 메모리 접근을 줄이기 위하여 메인 메모리 접근시점에 참조된다.
물론 둘 다 메인 메모리 접근을 줄이기 위함이라는 점은 비슷하다.

A cache stores a memory location temporarily while a TLB is like a cache that stores address translation (virtual to physical address)

단 이 TLB도 컨텍스트 스위칭이 일어날때 비워진다.

그 이유는 새로운 프로세스가 CPU를 할당받게 되면, 다른 메모리 주소공간을 참조할것이기 때문이다.
이때문에 컨텍스트 스위칭 직후 TLB 미스가 연속적으로 생긴다.

페이지 사이즈

페이지의 크기에 대해서도 얘기해보자.
페이지의 크기를 정하면, 페이지 테이블의 크기도 결정되므로 적절한 페이지 크기 선정이 중요하다.

여기서 말하는 적절한의 기준이 뭘까?

만약 모든 프로세스가 4K만 요구하는데 페이지 사이즈가 8K면?

모든 페이지에 4K만큼의 내부 파편화가 생기는 것이다.

• 만약 페이지 사이즈가 크다면?

  • 페이지 테이블의 크기는 줄어든다.
  • 한 개의 페이지 테이블안에 들어있는 데이터가 많으니 공간 지역성을 잘 만족한다.
  • 한 번에 많은 양의 데이터를 디스크에서 가져오니 I/O 작업이 줄어든다.
  • 내부 파편화 문제가 증가한다.
  • 필요하지 않은 데이터가 메모리에 올라올 수 있다.

• 만약 페이지 사이즈를 작다면?

  • 내부 파편화 문제가 감소한다.
  • 필요한 데이터만 메모리에 가져올 수 있다.
  • 공간 지역성을 지키기 어려워 페이지 폴트 발생 확률이 늘어난다.
  • 페이지 테이블 내의 엔트리가 많아지니 페이지 테이블의 크기가 커진다. 오버헤드가 발생한다.

따라서 여러가지 트레이드 오프를 고려해서 페이지의 크기를 정하는 것이 중요한데,
일반적으로 메모리 크기도 커지고, 프로세스 크기도 커져서 페이지 사이즈의 크기도 커지고 있다.

리눅스 16.04 기준 아래와 같은 명령어로 페이지 사이즈를 알 수 있는데 4096으로 4K다.

$ getconf PAGESIZE
> 4096