Why B 트리?
B 트리는 이진트리와 다르게 하나의 노드에 많은 정보를 가질 수 있는 트리를 의미한다. 노드의 최대 자식의 개수를 M이라고 할때, M차 B트리라고 한다.
B 트리는 고전적인 메모리 계층 구조의 물음에서 출발한다.
이진탐색트리의 시간복잡도가 최악이 될 때는 노드가 편향된 경우인데, 이를 해결하는 것이 AVL,RB 트리와 같은 균형이진트리다.
그런데 이것만으로 부족하다. 왜 그러냐면, O(logn) 을 보장하는 균형이진트리의 최악을 생각해보자.
최악이 있을까? 분명히 있다.
RB트리에서 원소가 1백만개라고 해보면, 트리의 높이는 최대 2*log(10^6)이다. 따라서 대략 20정도이다.
RB 트리에서 Red 노드는 최대 두개만 연속으로 되어있음을 생각하면 쉽게 알 수 있다.
그러면, 원하는 원소를 찾기 위해서 20번 정도의 노드 액세스가 필요한데,
만약 모든 노드가 메인 메모리에 있다고 생각해보면, 매우 비싼 20번의 메모리 접근이 일어나는 것이다.
심지어 메인 메모리가 아닌 디스크에 있다면? 더 많은 시간이 단순히 노드에 접근하는데 쓰일 것이다.
따라서 이러한 메모리, 디스크에 관한 접근을 줄여야 한다. 그러기 위해서는 트리의 탐색 높이를 줄여야 한다.
이진트리에서 log의 베이스가 2인 이유가 2개의 자식노드임을 기억했을때 degree를 늘려야 하는 것이다.
💡 실제로는 트리 노드들이 하나의 캐시 라인이나 디스크 블록을 채울 수 있는 가장 큰 차수를 사용하고 있다.
따라서 B 트리는 아주 많은 양의 데이터들이 존재하는 곳에 사용되고, 높이를 h 라고 할때, 조회,삽입,삭제 등등의 동작 모두 O(h) 의 디스크 접근을 요구한다.
B 트리는 노드에 가능한 최대의 키들을 삽입하면서 트리의 높이를 낮게 유지한다.
즉, Balanced를 삽입,삭제 과정에서 혼자서 유지한다는 것이다.
그렇기에 AVL,RB 트리와 비교해서 매우 낮은 디스크 접근을 수행한다.
💡 이게 뭔말인가 했더니 노드의 사이즈를 디스크 블록 사이즈와 거의 동일하게 유지한다는 말, 어차피 디스크 액세스할때 1K 읽나 , 1 Byte 읽나 오버헤드는 같으니까, 한번에 많이 읽어오면 되는거다.
이러한 여러가지 특성때문에 B 트리는 B+트리와 더불어서 DBMS에서 많이 사용되고 있다.
💡 인덱스 다룰때 많이 쓴다고 한다. 요즘에 MongoDB 만지는데 대놓고 공식문서에 인덱스는 B트리 쓴다고 되어 있다. 물론 PostgreSQL 이런건 B+트리도 쓰고, MySQL은 B 트리,B+트리, 해시 다 쓴다.
B 트리 정의
degree가 m인 B트리는 아래와 같은 특성을 가진다.
- 루트 노드는 적어도 2개의 자식을 가진다.
- 루트 노드와 외부 노드를 제외한 모든 내부 노드는 적어도
올림(m/2)개, 최대m개의 자식을 가진다.- m=2이면, 1~2개의 자식 노드 → 포화 이진 트리
- m=3이면, 2~3개의 자식 노드 → 2-3 트리
- m=4이면, 2~4개의 자식 노드 → 2-3-4 트리
- 모든 외부 노드들은 같은 레벨에 있다. (Perfectly Balanced)
- 이게 매우 중요... 높이의 상한을 준다는 것이니까 디스크 접근에 대한 상한을 준다는 것.
- 그림에서
{8,11}, {22,23}, {58,59}같은 애들을 외부 노드라고 부른다.
- 각각의 노드는 적어도
[m/2]개, 최대m-1개의 키를 가질 수 있다.- 아래 그림을 보면, m=3일때,
[3/2]=1~3-1=2개의 키를 가진다. 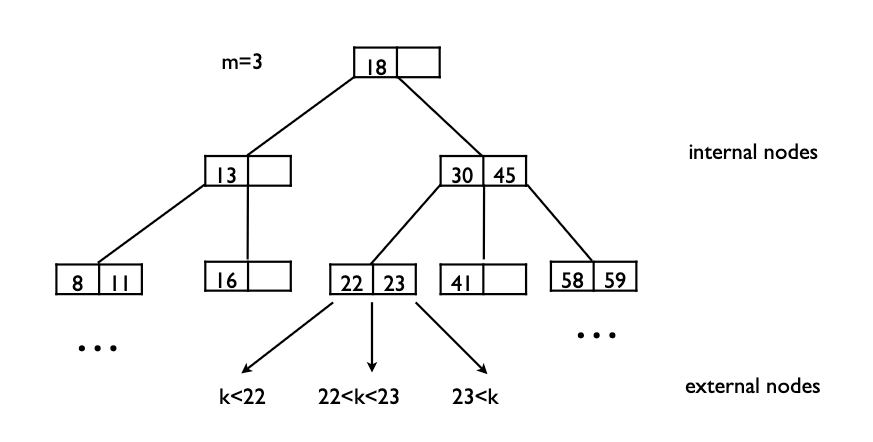
- 이런 조건이 있는 이유는, 만약 m=5일때 , 1개의 키가 있다고 해보자. 다음 키는 그 키보다 작거나 크거나 즉 두개인데, 그러면 3-4-5 트리를 만족하지 않는다.
- 아래 그림을 보면, m=3일때,
B 트리의 목적이 데이터를 넓게 흩뿌리면서 높이를 낮게 가져간다는 점을 생각해보면서, n개의 원소가 있다고 할 때, 높이의 상한에 대해서 계산해보자.
- Best Case
- 최고의 경우는 가장 잘 흩뿌려질때니
logm(n) n=(log n)/(log m)=O(log n)
- Worst Case
- 최악의 경우는 가장 덜 흩뿌려질때, 즉 노드가 최소의 자식을 가지는
올림(m/2)갈래로 흩어질때임. log올림(m/2)(n)=(log n)/(log(올림(m/2))=O(log n)
- 최악의 경우는 가장 덜 흩뿌려질때, 즉 노드가 최소의 자식을 가지는
즉 모든 최고,최악의 경우 모두 O(log n) 의 높이가 보장됨을 알게 되었다.
조회
조회는 이진탐색의 그것과 매우 비슷하다. 이진 탐색에서 조회는 분기가 세가지다. (못 찾는 경우 제외)
내가 찾는 키를 k 라고 하고, 노드의 키를 v 라고 하면,
k=v: 같거나 → 찾았다.k>v: 작거나 → 왼쪽 서브 트리로 간다.k<v: 크거나 → 오른쪽 서브 트리로 간다.
이것처럼 B 트리에서도 비슷한 방식대로 움직이는데, 분기가 두가지다.
k=v: 같거나 → 찾았다.i-th v< k < i+1-th v를 만족하는i를 찾고i-th pointer가 가르키는 서브트리로 간다.- 이때 만족하는
i는 최대m-1개이므로, 루프를 돌아도 되고, 이진 탐색을 수행해도 된다. ← 루프를 돌아도 안전한게, 어차피 같은 메모리안에 올라와
있다. 추가적인 디스크 액세스가 필요하지 않다.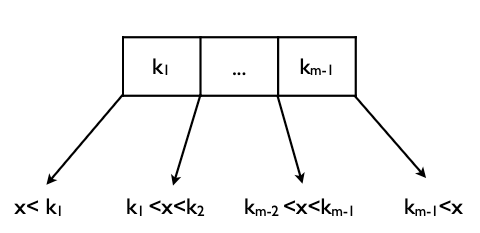
- 이때 만족하는
삽입
삽입부터 B 트리가 복잡해지고, 또 그 과정에서 B 트리가 가지는 균형유지의 전략을 볼 수 있다.
일단, 조회의 과정을 거치고, 삽입할만한 적절한 리프 노드 위치를 찾는다. 그 다음부터 분기가 나뉜다.
💡 리프 노드에 넣는 이유는 아래에서 설명하겠지만 삽입시에 일어나는 분할이 상향식이기 때문이다.
- 삽입할 곳에 자리가 남아있다면 (
current capacity<m-1) , 그냥 넣고 끝낸다. - 삽입한 뒤에 넘친다면, 분할한다.
분할
리프노드에 삽입한 후에 m개의 키를 가진다면, 분할하는 과정을 거친다. m개의 키를 가진 노드에 대해서 세 그룹으로 분할한다. (아래 과정은 m이 홀수일때)
- 중위순서의 키보다 작은 키들로 이루어진 노드들
- 중위순서의 키
- 중위순서의 키보다 큰 키들로 이루어진 노드들
그리고 1번과 3번 그룹의 부모를 2번으로 만든다. 즉, 여전히 성질이 깨지지 않게끔 하는 것.
만약 이때 부모가 넘친다면? 또 다시 진행한다. 그렇기에 리프노드에서의 넘침이 상향식으로 전파될 가능성이 있는것.
이게 루트까지 넘친다면, 루트에 대해서 두 개의 자식을 가지는 새로운 노드를 만든다.
예시를 다 보여주기에는 어려우니, 가장 복잡한 예시만 들면 아래와 같다.
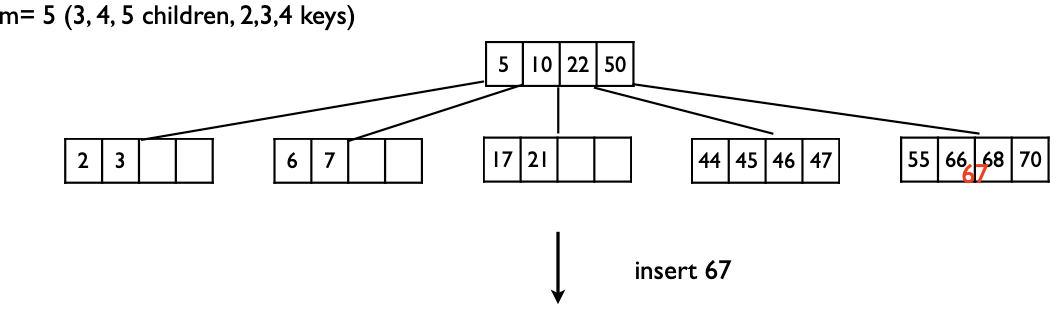
우선 67이 들어갈 위치를 찾는 과정을 거치고, 넣을만한 곳을 찾았는데 넣는 순간 5개의 키를 가지면서 넘친다. 분할 발생!
중위순서의 키는 67이니, {55,66}, {67}, {68,70} 로 나눈 후 {55,66} → {67} ← {68,70} 으로 만든다.
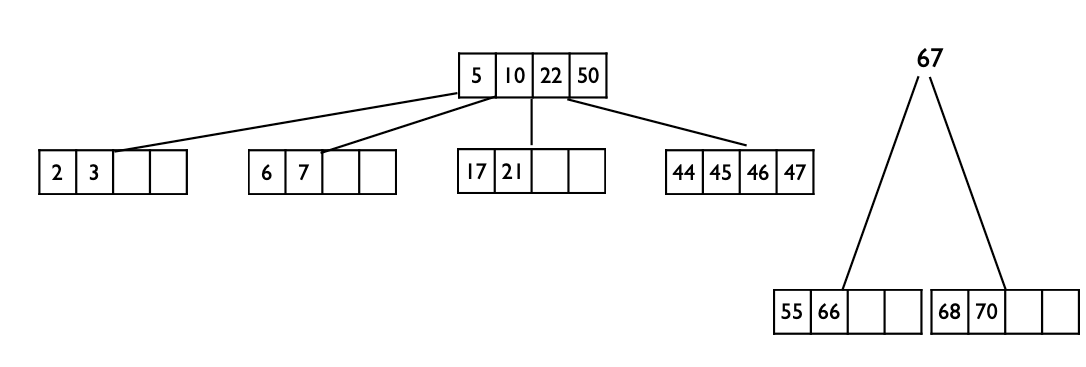
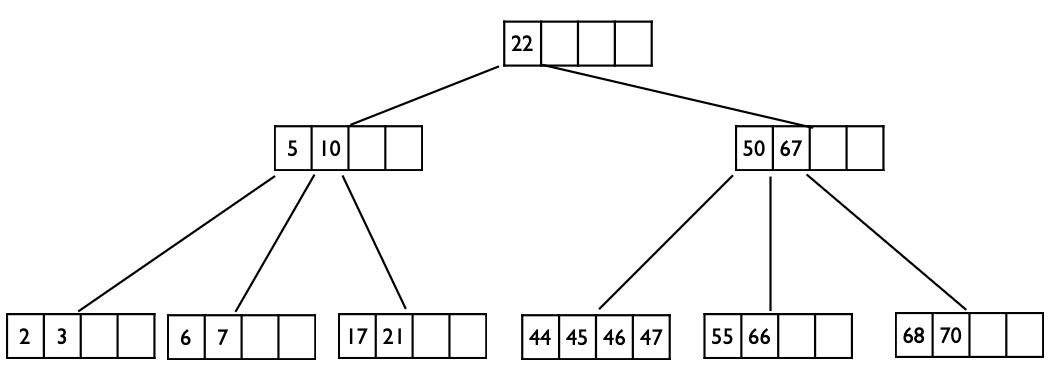
근데 67이 들어갈 위치는 50의 옆이다. 그런데 그럼 루트에서 넘침이 생기니, 루트에 대해서 상향식으로 분할이 전파된다.
따라서 {5,10} → {22} ← {50,67}의 구조로 만든 후 체크하면 5개의 키를 안 넘치니 끝.
삭제
삭제는 삽입보다 복잡하다.
B트리에서의 삭제는 삭제된 후에 B트리의 성질을 유지하기 위해서 최소키의 개수를 만족하는지,
만족하지 않으면 추가적인 조치가 필요하기 때문이다.
B트리에서의 삭제는 크게는 두가지, 작게는 세가지 경우가 있는데 , 먼저 삭제할 키인 k가 리프에 있는지 없는지를 따져서 두가지로 나뉜다.
💡 모든 삽입, 삭제 과정에서
k가 들어갈 혹은 삭제될 위치를 찾는 조회과정이 선행된다.
k가 리프에 있을때
근데 여기서 또 나뉜다. 골치 아프다. 아래 과정에서 m은 3이다. (2-3트리)
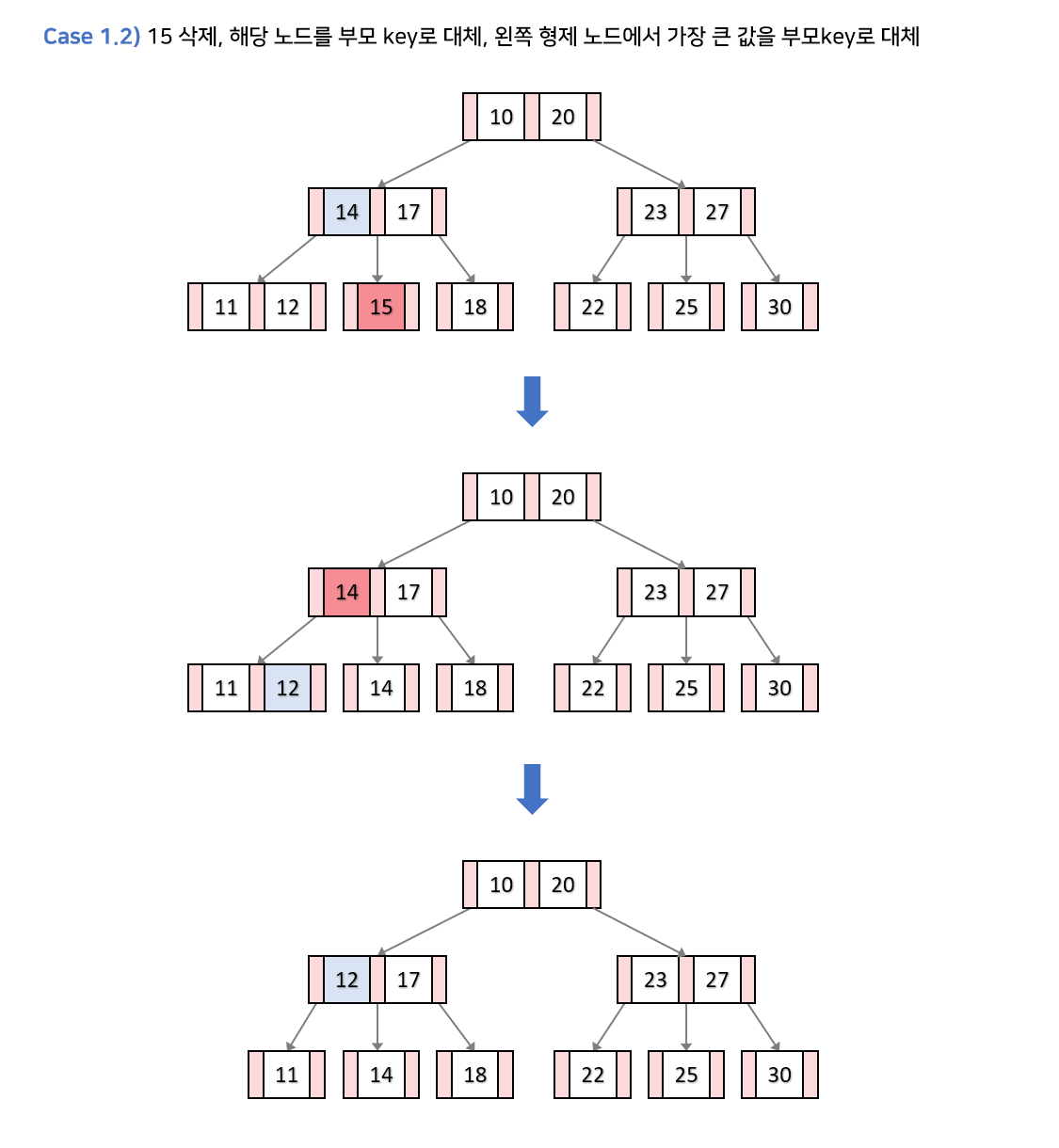
k가 있는 노드의 키의 개수가 최소 키의 개수보다 클때 → 그냥k를 삭제해도 아무런 문제가 없다.- 형제 노드 중 하나의 키의 개수가 최소 키의 개수보다 클때
- 부모 키의 값으로
k를 대체한다. - 최소 키의 개수보다 큰 형제노드가 왼쪽 형제라면 가장 큰 값을, 오른쪽 형제라면 가장 작은 값을 부모 키로 대체한다.
- 부모 키의 값으로
- 양 쪽 형제가 최소 키의 개수를 가지고 있고 , 부모 노드의 키가 최소 키의 개수보다 많다면,
k를 삭제한 후, 부모 키와 형제 노드를 병합한다. → 정확히는 부모 키가 내려오는 것.- 부모노드의 키를 하나 줄이고, 자식 수 역시 줄여서 B트리의 특성을 유지한다.
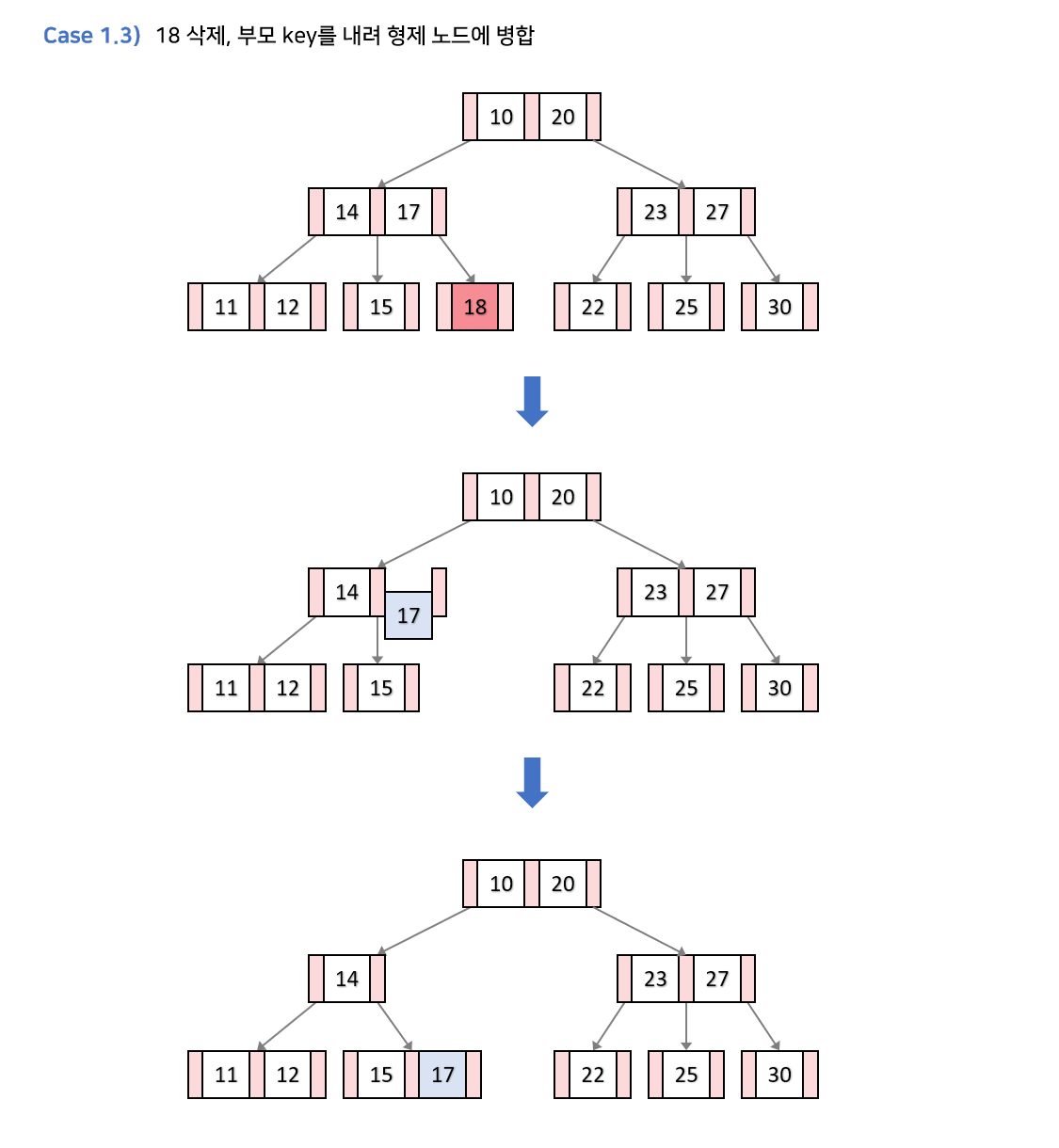
- 양 쪽 형제가 최소 키의 개수를 가지고 있고, 부모 노드 역시 최소 키의 개수면 → 부모를 루트로 한 서브 트리의 높이 자체가 줄어들기 때문에 재구조화가 이어진다. 아래 참조
- 어디에서 가져오든, 무조건 빵꾸가 생기잖아요~
k가 내부노드에 있고, 현재 노드 혹은 자식 노드의 키의 개수가 최소 이상일때
k를 predecessor(왼쪽 서브트리의 가장 큰 값) 혹은 successor(오른쪽 서브트리의 가장 작은 값)와 교환해준다. 찾는 과정은 BST의 그것과 매우 유사.
그런 후에 리프 노드가 된 k 를 삭제한 후 필요에 의해서 리프노드에서의 삭제 핸들링 과정으로 넘어간다.
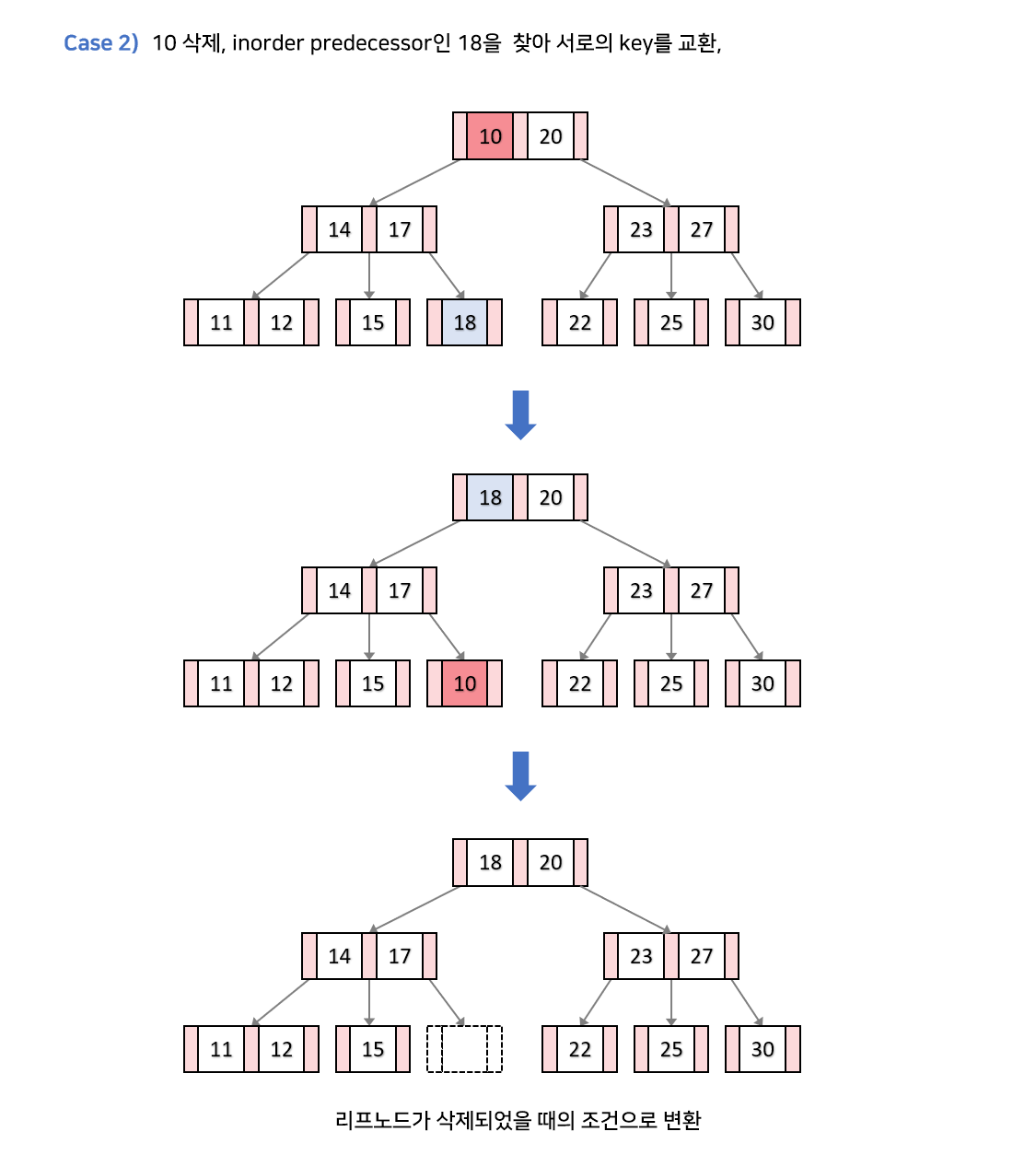
위의 그림에선, 양쪽 형제 모두 최소 키의 개수만큼 가지고 있고, 부모노드의 키의 개수가 최소개수 이상이니 15,17이 병합된다.
k가 내부노드에 있고, 현재 노드,자식 노드의 키의 개수가 최소개수일때
만약 이 상황에서 k를 삭제하면, 전체적인 높이가 낮아지면서 B 트리의 조건을 유지하려 함. 이를 트리의 재구조화라 한다.
k를 삭제하고,k의 자식을 하나로 합친다.k의 부모 키를 인접한 형제노드에 붙인다. (이때k는 당연히 루트가 아니다. 루트면 위에서 걸렸겟지)- 아까 병합한 노드를 2번의 자식노드로 설정한다. (왼쪽 혹은 오른쪽)
- 만약 이럴때, 부모노드의 키의 개수에 따라 수행 과정이 다르다. 이에 대해서 또 분기한다.
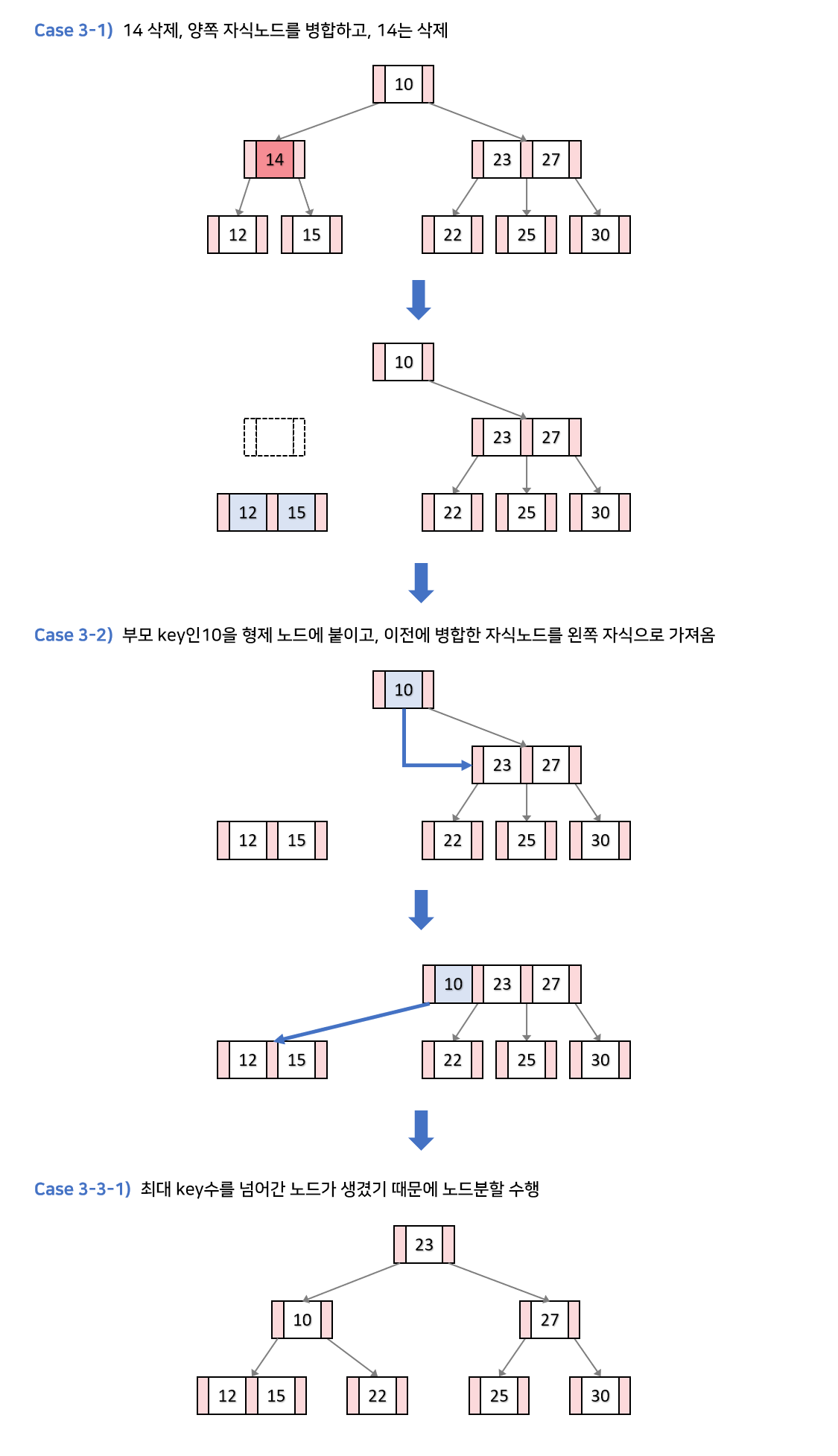
- 새로 구성된 인접 형제노드(부모 키 붙인)가 오버플로우 나면, 삽입연산에서의 분할 수행
- 인접 형제노드가 구성되더라도,
k의 부모 노드가 최소 키의 개수보다 작아진다면, 다시 위의 2번 과정부터 수행한다.
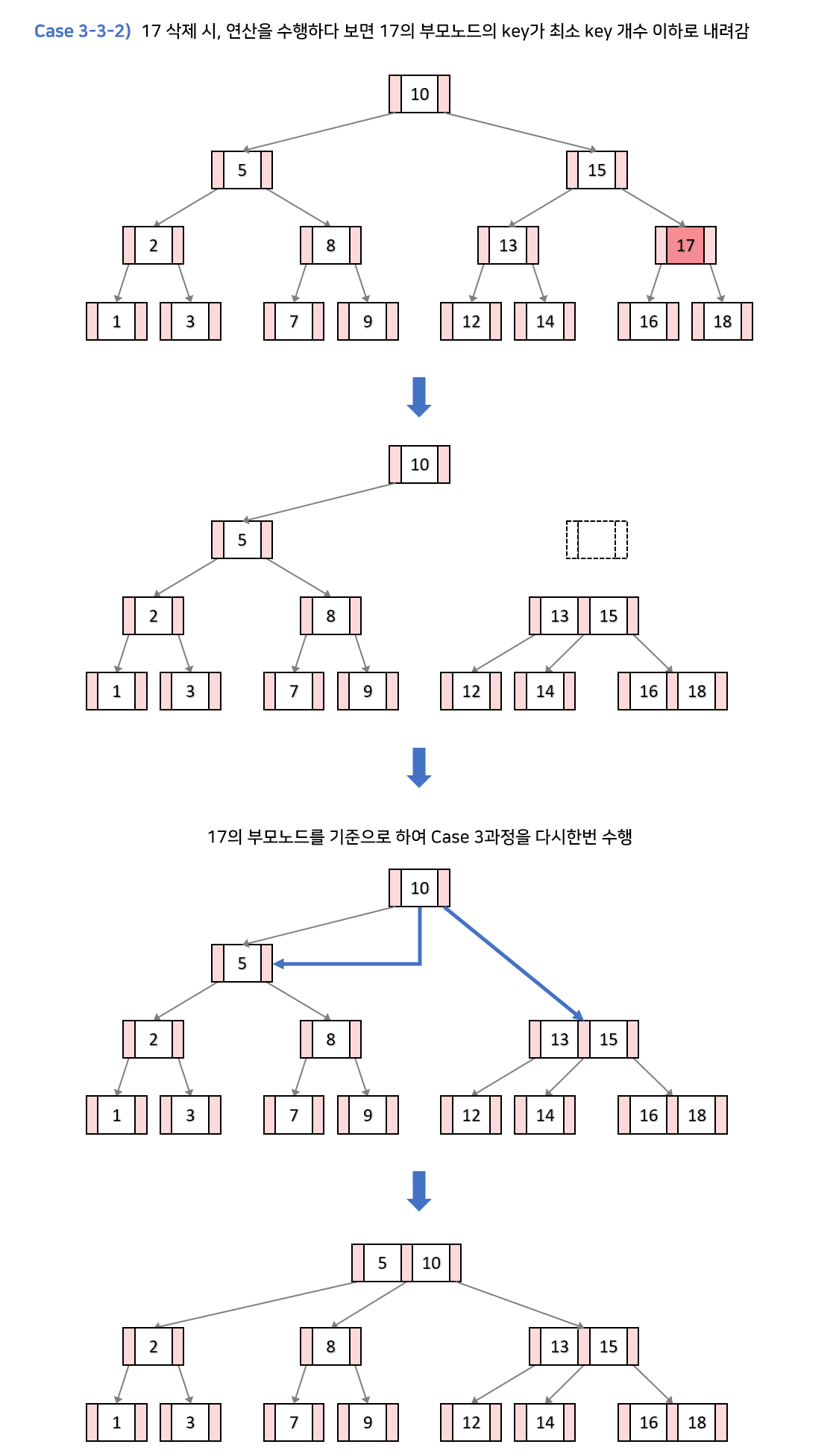
다른 예시
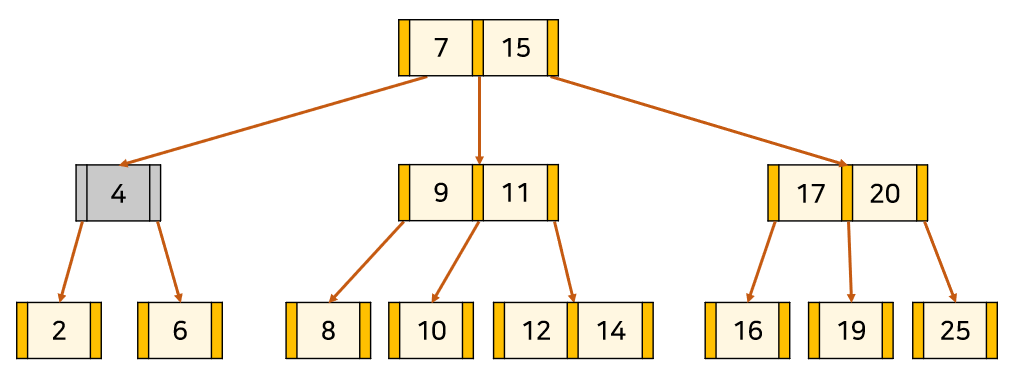
4를 삭제하자. 이러면 현재 노드, 자식 노드 모두 키가 최소다.
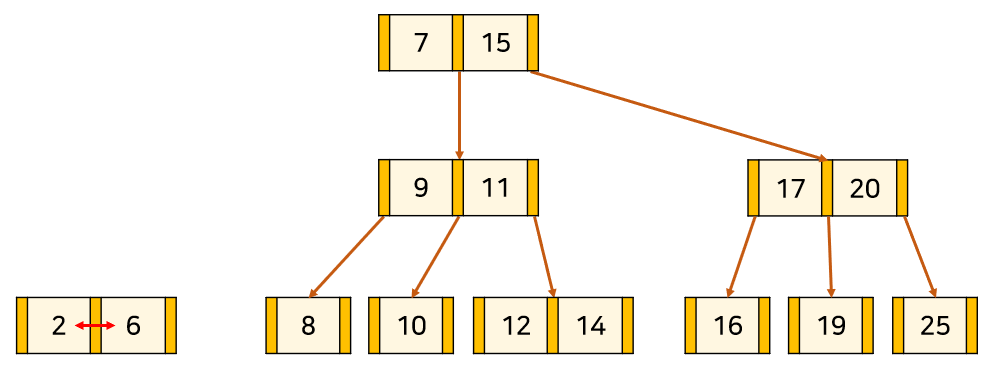
2와 6을 합치고,
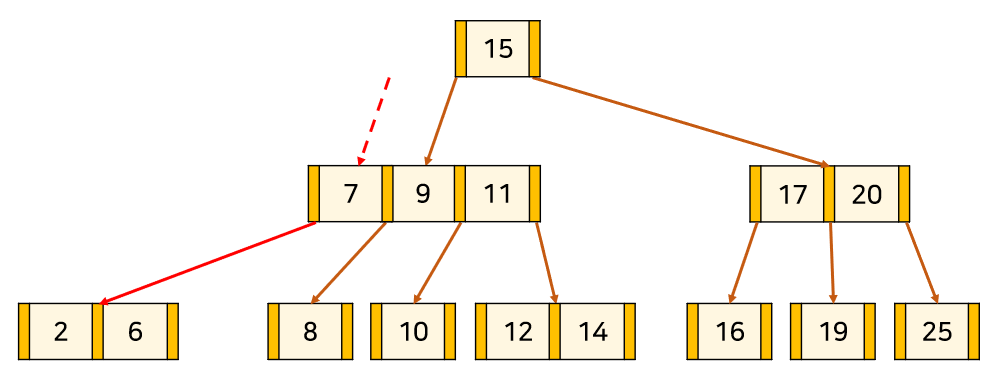
내 부모 노드와 합친것을 자식-부모관계로 연결시켜준다.
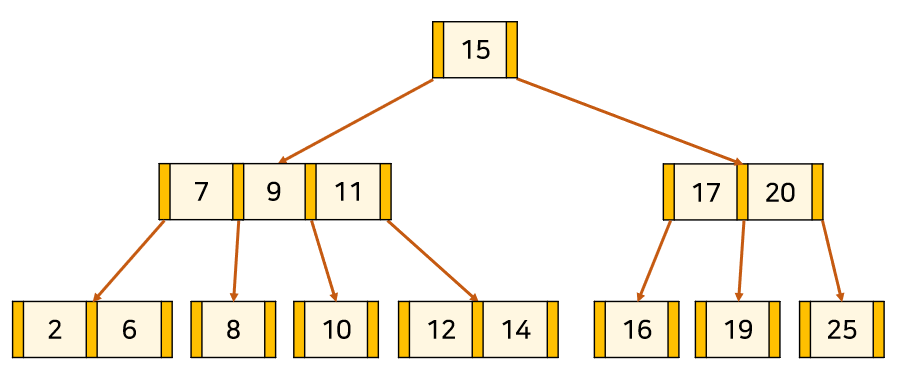
이때 7,9,11이 오버플로우가 나니 중앙값인 9를 분할해 처리한다.
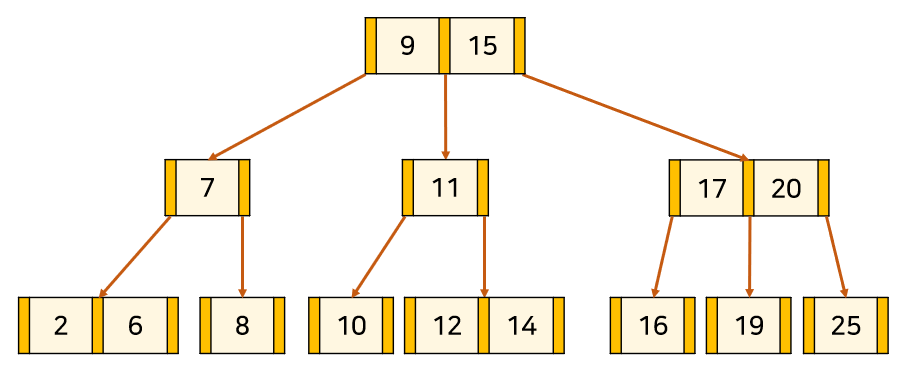
당연하게도 9,15에 대해서 분할의 propagation이 일어날 수 있다.
차수에 대한 고민
결국에 높이를 최대한 낮춘다는 것이 B 트리의 성능 개선점이라고 보았을때, 차수(degree 혹은 order)를 잘 고르는 것이 중요하다.
좋은 차수를 고르는 방법은, 페이지 사이즈에 꽉 맞춰 들어가는 최대한 큰 사이즈의 노드를 고르는 것이다.
만약에 디스크에서 읽어오는 데이터베이스를 B 트리를 통해서 구성하려 한다면,
각각의 노드가 디스크 페이지 크기에 딱 맞는 사이즈를 골라야 할 것이다.
만약에 In-memory 데이터베이스를 구성하려 한다고 해보자.
그 말은 데이터는 메모리<->메모리 간 이동이 많을 것이고 중간에 L2 혹은 L3 캐시에 적재될때가 가장 빠른 접근을 할 수 있을때이다.
따라서 최대한 캐시 효율을 누릴 수 있게 L2나 L3 캐시의 라인 사이즈에 맞게끔, 즉 초과해서 캐시 바깥의 노드를 읽을 필요가 없게끔 구성해야한다.
모든 케이스에서 어떤 차수를 사용하는지 고르기 전에 먼저 하드웨어에 대한 스펙을 봐야할것이고,
내가 구현하려는 기능에서 B 트리가 어떤 역할을 하는지 알아야 할 것이다.
💡 Typically, you'd choose the order so that the resulting node is as large as possible
while still fitting into the block device page size.
If you're trying to build a B-tree for an on-disk database, you'd probably pick the order
such that each node fits into a single disk page,
thereby minimizing the number of disk reads and writes necessary to perform each operation.
If you wanted to build an in-memory B-tree, you'd likely pick either the L2 or L3 cache line sizes as your target
and try to fit as many keys as possible into a node without exceeding that size.
In either case, you'd have to look up the specs to determine what size to use.
강점
B 트리가 어떻게 균형을 유지하는지는 알았는데 실용적으로 어떤 강점이 있을까?
HashTable의 grow 된다는 점을 생각하지 않았을때, O(1) 이어서 더 유리한거 아닌가?
분명한 건 해시테이블을 이용할때는 하나의 조회에 있어서 O(1)이 소요되는것은 맞다.
하지만, 이 조회는 어디까지나 Hash Table.eqaul(key) 의 결과물이지 DB에서 쓰이는 range 와 같은 연산을 수행하지 못한다.
💡 실제로 회사에서 설계를 하면서 Redis를 사용하자는 의견이 나왔을때, 이 근거로 반대했다.
range연산이 필요한 곳에서는 HashTable에 기반한 redis는 전혀 이점을 누릴 수 없다.
즉, range 와 같은 연산을 수행할때는 계속된 참조가 필요한 것이다. 또, 해시테이블에서 특별한 구현체를 제외하고는 일반적으로 데이터가 정렬되어 있지 않다. 그렇기에 range 와 같은 연산이 매우 비효율적인것이다.
그럼 해시테이블과 비교했을때 강점에 대해서는 알았는데, 다른 트리랑 비교하면 어떨까?
다른 트리에서도 O(log n) 을 지원하는데 그건 왜 사용되지 않을까?
앞서 말한 높이의 상한에 있어서의 엄격함과 더불어서 B 트리의 노드들의 데이터는 배열속에서 순차적으로 저장되어 있고,
연속적으로 메모리에 저장되어 있음을 뜻한다. 즉, 공간지역성이 높다는 것이다.
다시 말해서, B 트리노드 끼리 참조로 이동할때는 디스크 액세스가 필연적이지만, 노드 내부의 데이터들은 배열과 같은 구조로 저장되어 있기 때문에 Sequential access에 유리하다. 이는 공간지역성에 의해서 캐시효율이 높음을 의미한다.
그렇기에 같은 O(log n) 의 시간복잡도를 가져도, 다른 트리보다 빠른 접근이 가능한 것이다.
다른 트리는 노드끼리 이동할때 자연스럽게 추가적인 메모리 접근이 필요하지만, B 트리에서 노드 안의 데이터 접근은 공간지역성을 충분히 누릴 수 있다는 것.
정리하자면,
- 항상 정렬된 상태이기에 부등호 연산에 유리하다.
- 참조 포인터가 적어 빠르게 메모리 접근이 가능하다.
- 데이터 탐색뿐 아니라 삽입, 삭제에도
O(h) = O(log n)의 시간 복잡도를 가진다.#define order 3 struct B_node { int order; /* number of children / B_node *child[order]; / children pointers / int key[order-1]; / keys */ }
```
💡 그런데 이제 h에 밸런싱을 곁들인...
요즘 MongoDB에 대해서 빡세게 사용중인데, 정말 자료구조가 중요함을 새삼 느낀다.
백엔드 개발자가 DB 모르는건 말이 안되니까.
'자료구조' 카테고리의 다른 글
| Stack과 Queue (0) | 2022.09.18 |
|---|---|
| Array와 Linked List (0) | 2022.09.18 |
| Hash Table에 대해서 완전 자세하게 알아보자. (0) | 2022.09.18 |
| Hash Table에 대해서 완전 자세하게 알아보자. (0) | 2022.04.09 |